4.1 확률적 경사 하강법
손실함수의 곡면에서 '경사가 가장 가파른 곳으로 내려가다 보면 언젠가 가장 낮은 지점에 도달한다'의 가정으로 만들어졌다. 하지만 여러 문제점이 있었다.
1)고정된 학습률
확률적 경사하강법은 지정된 학습률을 사용하는 알고리즘이다. 학습률이란 최적화할때 한걸음의 폭을 결정하는 스텝 크기를 말하며 학습속도를 결정한다. 이때문에 최적화가 비효율적으로 진행된다.
일반적으로 학습초기에는 큰폭으로 이동해 빠르게 이동하고 어느정도 이동하면 작은폭으로 천천히 이동해 최적해에 조심스럽게 이동해야한다. 이와 같이 학습의 진행상황이나 곡면의 변화를 알고리즘 내에서 고려해서 학습률을 자동으로 조정하는 방식을 적응적 학습률이라고 한다.
2) 협곡에서 학습이 안되는 문제
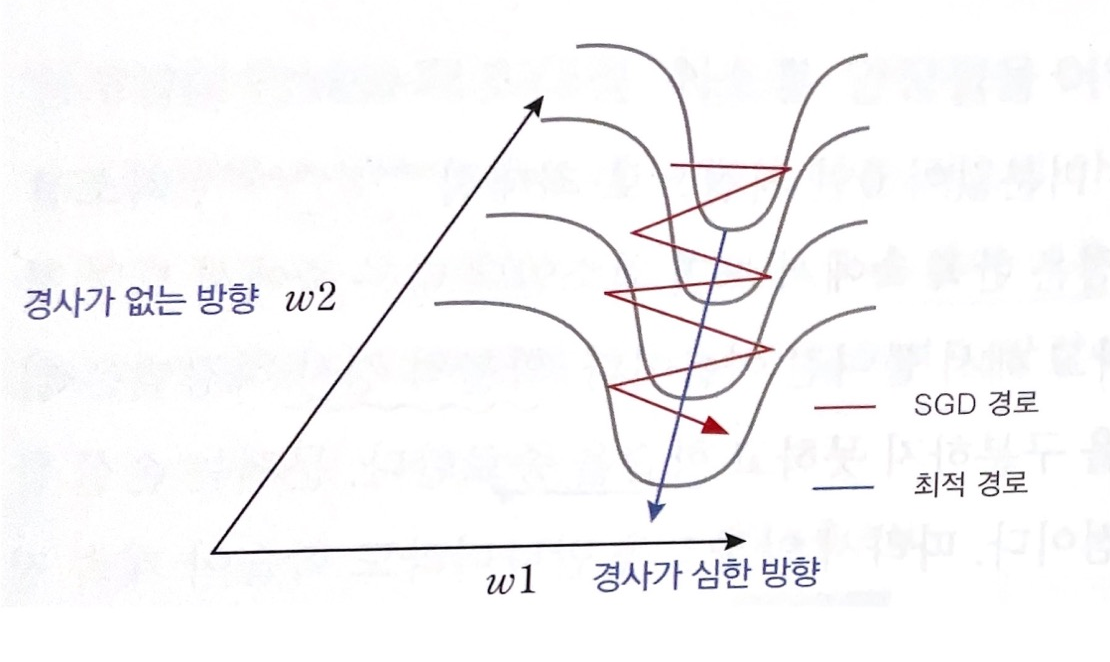
다음과 같이 가로방향으로는 경사가 매우 가파르고 세로방향으로는 경사가 거의없는 폭이 좁고 깊은 협곡인 경우 확률적 경사하강법이 이러한 지형을 만나면 진동만하고 아래쪽으로 잘 내려가지 못한다. 이는 1차 미분인 기울기만 사용하면 장축을 따라 매끄럽게 진행될 수 없어서 생기는 일로 기울기만 사용해야 한다면 진행하던 속도+관성을 추가해 덜 진동하게 만들 수 있다.
3)안장점에서 학습종료
손실함수 곡면에는 미분값이 0인 임계점으로 최대점, 최소점, 안장점이 있다. 안장점은 한쪽 축에서 보면 최소인데 한쪽 축에서 보면 최대인 지점이다. 이는 손실로 확인해보면 최대점이 손실이 매우 크고 최소점은 손실이 낮으며 안장점은 손실이 높은 편이다. 이는 진행하던 속도에 관성을 주면 안장점에서 쉽게 탈출할 수 있다.
4)학습 경로의 진동
확률적 경사하강법은 기울기가 자주바뀌는 거친 표면에서 이동하면 최적화 경로가 진동한다.최적화 경로가 최적해를 향해 일관성 있게 진행하려면, 손실함수의 표면이 거칠더라도 민감하게 경로를 바꾸지 말아야 한다.
4.2 SGD모멘텀
SGD+관성. 현재 속도벡터와 그레디언트 벡터를 더해 다음위치를 정한다. 관성이 작용하면서 학습경로가 전체적으로 매끄러워지고 가파른 경사를 만나면 가속도가 생겨서 학습이 매우 빨라진다
Vt+1 = ρvt+∇f(xt) ρ:마찰계수 0.9,0.99사용
Xt+1 = xt-αvt+1
다음 속도는 현재속도에 마찰계수를 곱한 뒤 그레디언트를 더해서 계산한다.
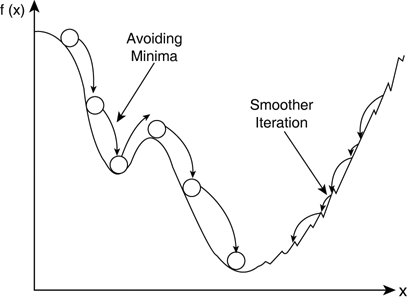
SGD모멘텀은 오버슈팅이 되는 단점이 있다. 경사가 가파르면 빠른 속도로 내려오다가 최소지점을 만나면 그레디언트는 순간적으로 작아지지만 속도는 여전히 크기 때문에 최소지점을 지나쳐 오버슈팅이 된다.
4.3 네스테로프 모멘텀
SGD모멘텀과 같이 진행속도에 관성을 주는 것은 같지만 오버슈팅을 막기 위해 현재속도로 미리 한걸음 가보고 오버슈팅된만틈 그레디언트로 조정해 이동방향에 차이가 있다.
Vt+1 = ρVt-α∇f(Xt+ρVt) ρ:마찰계수 Xt+ρVt:한걸음 미리 가기
Xt+1 = Xt+Vt+1

4.4 AdaGrad (adaptive gradient)
손실함수의 곡면의 변화에 따라 적응적 학습률을 정하는 알고리즘. 손실함수의 경사가 가파를 때는 작은폭으로 이동하고 경사가 완만하면 큰 폭으로 이동하도록 적응적으로 학습률을 조정한다.
rt+1 = rt+∇f(xt)^2
xt+1 = xt-α/√rt+1 + ε ⊙∇f(xt)
밑줄이 곡면의 변화량을 반영하는 적응적 학습률이다.AdaGrad는 모델의 파라미터별로 곡면의 변화량을 계산하기 때문에 파라미터별로 개별 학습률을 갖는 효과가 생긴다.
하지만 한가지 치명적인 문제가 있는데 곡면의 변화량을 전체 경로의 기울기 벡터로 계산하므로 학습이 진행될수록 곡면의 변화량을 점점커지고 반대로 적응적 학습률은 점점 낮아서 조기에 학습이 중단될 수 있다.
4.5 RMSProp
최근 경로의 곡면 변화량에 따라 학습률을 적응적으로 정하는 알고리즘이다. AdaGrad가 조기에 학습이 중단되는 문제를 해결하기 위해 RMSProp은 곡면 변화량을 개선된 방식으로 측정한다. 이 알고리즘은 지수가중이동평균을 사용한다. rt+1을 rt와 그레디언트의 제곱 ∇f(xt)^2을 가중합산해서 지수가중이동평균을 계산했다.
rt+1 = βrt+(1-β) ∇f(xt)^2
xt+1 = xt-α/√rt+1 + ε ⊙∇f(xt)
RMSprop을 점화식으로 풀어보면 현재시점에서 멀어질수록 가중치가 1,β1,..βt-2,βt-1와 같이 점점 0에 수렴한다. 따라서 최근 경로의 그레디언트는 많이 반영되고 오래된 경로의 그레디언트는 작게 반영된다.
4.6 Adam
SGD모멘텀 + RMSProp. 관성에 대한 장점과 적응적 학습률에 대한 장점을 모두 갖는다. 최적화 성능이 우수하고 잡음 데이터에 대해 민감하게 반응하지 않는 성질이 있다. 첫반째 식은 1차관성으로 속도를 계산한다. SGD모멘텀의 첫번째 식이지만 속도에 마찰 계수 대신 가중치를 곱해서 그레디언트의 지수가중이동평균을 구하는 형태로 수정되었다. 두번째 식은 2차 관성으로서 그레디언트 제곱의 지수가중이동평균을 구하는 식이다. 세번째 식은 파라미터 업데이트식으로 1차관성과 2차관성을 사용한다.
vt+1 = β1vt+(1-β1)∇f(xt)
rt+1 = β2rt+(1-β2)∇f(xt)^2
xt+1 = xt-α/√rt+1 + ε ⊙vt+1
'Deep learning' 카테고리의 다른 글
| Do it!딥러닝 교과서 chapter 6. 콘벌루션 신경망 (0) | 2022.05.11 |
|---|---|
| Do it 딥러닝 교과서 chapter 5: 초기화와 정규화 (0) | 2022.05.09 |
| Do it!딥러닝 교과서 chapter3 :신경망 학습 (0) | 2022.04.08 |
| Do it! 딥러닝 교과서 chapter 2 순방향 신경망 (0) | 2022.04.05 |
| Do it 딥러닝 chapter1. 딥러닝 개요 (0) | 2022.04.01 |